3. 1.-
Problemas de
![]() y
y
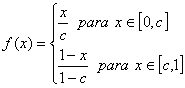
Decimos que ![]() es un punto n-periódico si
es un punto n-periódico si ![]() y n
es el menor número con esta propiedad. Prueba que para todo
y n
es el menor número con esta propiedad. Prueba que para todo ![]() el conjunto de n-periódicos es no vacío y finito.
el conjunto de n-periódicos es no vacío y finito.
(1998-Segundo día, Problema 3)
Solución
Como ![]() es una ecuación de grado uno, y hay como
máximo
es una ecuación de grado uno, y hay como
máximo ![]() ecuaciones diferentes para cada n, el número de puntos en cada conjunto
de n-periódicos es finito.
ecuaciones diferentes para cada n, el número de puntos en cada conjunto
de n-periódicos es finito.
Tenemos que demostrar que hay al menos una solución en cada
conjunto. Puesto que ![]() se tiene como
máximo para
se tiene como
máximo para ![]() puntos como
dijimos arriba, tenemos que el máximo número de puntos de periodo menor ó igual
que
puntos como
dijimos arriba, tenemos que el máximo número de puntos de periodo menor ó igual
que ![]() es
es ![]() , así que al menos 2
puntos tienen exactamente periodo n.
, así que al menos 2
puntos tienen exactamente periodo n.
Observación
Faltaría ver, para acabar la
demostración del problema según el enunciado de la IMC,
que ![]() se tiene
exactamente para
se tiene
exactamente para ![]() puntos
puntos
12.- ¿Existe una aplicación biyectiva ![]() tal que
tal que ![]() ?
?
(1999-Primer día, Problema 2)
Solución
Sea ![]() una biyección. Entonces tenemos dos
secuencias:
una biyección. Entonces tenemos dos
secuencias:
![]() .
Ahora si aplicamos la desigualdad de
reagrupamiento podemos asegurar que
.
Ahora si aplicamos la desigualdad de
reagrupamiento podemos asegurar que ![]() es mínimo si
es mínimo si ![]() y
y ![]() están ordenados en
orden inverso. Como
están ordenados en
orden inverso. Como ![]() es una sucesión
decreciente, tenemos que
es una sucesión
decreciente, tenemos que
![]() ,
luego no existe tal biyección.
,
luego no existe tal biyección.
13.- Supongamos que una función ![]() satisface la desigualdad
satisface la desigualdad
![]()
Probar que ![]() es una función constante.
es una función constante.
(1999-Primer día, Problema 3)
Solución
Sea ![]() . Entonces es fácil ver que:
. Entonces es fácil ver que:
![]()
![]() .
Supongamos que existe un punto
.
Supongamos que existe un punto ![]() en el que
en el que ![]() .
Entonces, cojamos
.
Entonces, cojamos ![]() tal que
tal que
![]() .
.
Sea n un entero con
la propiedad de que ![]() y
y ![]() . Por tanto,
. Por tanto, 
Esto da una contradicción y por tanto ![]()
![]() , y
entonces
, y
entonces ![]() luego con
luego con ![]() ,
conseguimos
,
conseguimos ![]() luego f
es una función constante.
luego f
es una función constante.
14.- Supongamos que ![]() y
y ![]() .
Probar que
.
Probar que ![]()
(1999-Segundo día, Problema 3)
Solución
Sabemos que ![]() ,
luego
,
luego
![]()
![]()
15.- Sea ![]() un entero positivo. Consideremos una matriz
un entero positivo. Consideremos una matriz ![]() con entradas
con entradas ![]() escritos en orden
empezando por la esquina arriba a la izquierda y siguiendo por cada fila de
izquierda a derecha. Elegimos
escritos en orden
empezando por la esquina arriba a la izquierda y siguiendo por cada fila de
izquierda a derecha. Elegimos ![]() entradas de la matriz
tales que exactamente hay una en cada fila y columna. ¿Qué valores posibles
puede tomar la suma de los elementos seleccionados?
entradas de la matriz
tales que exactamente hay una en cada fila y columna. ¿Qué valores posibles
puede tomar la suma de los elementos seleccionados?
(2001-Primer día, Problema 1)
Solución
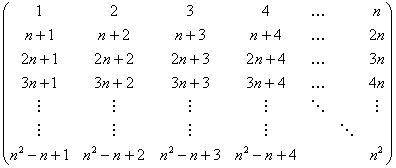
Si cogemos un número de cada fila y de cada columna, la suma
será ![]() . Como
. Como
![]() entonces
entonces ![]() . Como
hemos seleccionado un número de cada columna,
. Como
hemos seleccionado un número de cada columna,
![]()
16.- Sean ![]() enteros positivos
primos dos a dos.
enteros positivos
primos dos a dos.
a) Si ![]() y
y ![]() son elementos de un
grupo conmutativo con elemento unidad
son elementos de un
grupo conmutativo con elemento unidad ![]() , y
, y ![]() ,
prueba que
,
prueba que ![]() .
.
b) ¿Es cierta la conclusión si ![]() y
y ![]() son elementos de un
grupo no conmutativo cualquiera?
son elementos de un
grupo no conmutativo cualquiera?
(2001-Primer día, Problema 2)
Solución de a)
Sea m el menor natural
tal que ![]() y n
el menor natural tal que
y n
el menor natural tal que ![]() .
Entonces
.
Entonces ![]() , y
como
, y
como
![]() ,
tenemos que
,
tenemos que
![]()
Pero ![]() es el menor natural
que cumple
es el menor natural
que cumple ![]() , luego n| t m.
Sin embargo, como n| s y m|
r, tenemos que n, m, t son primos entre sí, así que n=1. Se sigue igualmente que m=1, luego a=b=e.
, luego n| t m.
Sin embargo, como n| s y m|
r, tenemos que n, m, t son primos entre sí, así que n=1. Se sigue igualmente que m=1, luego a=b=e.
17.- Supongamos que las funciones diferenciables ![]() satisfacen
satisfacen
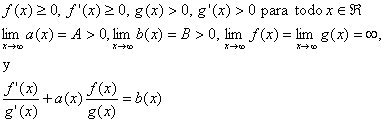
Prueba que
![]()
(2001-Primer día, Problema 6)
Solución
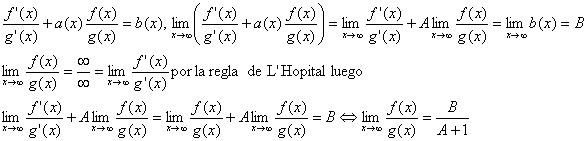
Como para aplicar la regla de L’Hopital
necesitamos saber que existe el ![]() , tenemos que ver si existe
, tenemos que ver si existe ![]() , ya que en ese caso, tomando límites en la igualdad:
, ya que en ese caso, tomando límites en la igualdad: ![]() tenemos que
tenemos que
![]() , y por tanto existe
, y por tanto existe ![]() .
.
Nota: Faltaría demostrar que ![]() existe.
existe.
18.- Sea ![]() una función con
derivadas de cualquier orden en
una función con
derivadas de cualquier orden en ![]() y tal que existe
y tal que existe ![]() para todo
para todo ![]() . Demuestra que si
. Demuestra que si ![]() tiene una asíntota
horizontal en
tiene una asíntota
horizontal en ![]() , entonces
, entonces ![]() . ¿Es el recíproco cierto?
. ¿Es el recíproco cierto?
(2005-Lista Corta, Problema 42)
Solución
Demostraremos que es cierto para ![]() . Tenemos que
. Tenemos que ![]() , y por otro lado, por el teorema de Lagrange
tenemos que
, y por otro lado, por el teorema de Lagrange
tenemos que
![]() . Por tanto si tomamos límites a ambos miembros de la
expresión tenemos que:
. Por tanto si tomamos límites a ambos miembros de la
expresión tenemos que:
![]() .
.
Demostremos ahora que si para un cierto ![]() se tiene que
se tiene que ![]() entonces para
entonces para ![]() también es cierto.
también es cierto.
Tenemos nuevamente por el teorema de Lagrange, que al existir
todas las derivadas de ![]() , entonces
, entonces ![]() y por tanto
y por tanto
![]() así que queda probado.
así que queda probado.
Para demostrar que el recíproco es falso basta considerar ![]() .
.
Nota:
Sí que se puede afirmar que, si ![]() , entonces
, entonces ![]() (de hecho, con que
(de hecho, con que ![]() basta):
basta):
Si ![]() , entonces
, entonces ![]() y usando nuevamente el
teorema de Lagrange, tenemos que
y usando nuevamente el
teorema de Lagrange, tenemos que ![]() y
y
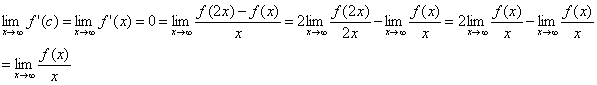
19.- Sea ![]() una matriz simétrica
con autovalores distintos y sea
una matriz simétrica
con autovalores distintos y sea ![]() el conjunto de todas
las matrices
el conjunto de todas
las matrices ![]() tales que conmutan con
tales que conmutan con
![]() ,
, ![]() . Demuestra que las matrices de
. Demuestra que las matrices de ![]() son también
simétricas. ¿Es el resultado cierto si
son también
simétricas. ¿Es el resultado cierto si ![]() tiene autovalores
múltiples?
tiene autovalores
múltiples?
(2005-Lista Corta, Problema 33)
Solución
Vemos primero que si ![]() tiene autovalores
múltiples el resultado es falso: con
tiene autovalores
múltiples el resultado es falso: con 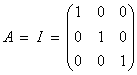 ,
, ![]() sería el conjunto
de todas las matrices, y no todas son simétricas.
sería el conjunto
de todas las matrices, y no todas son simétricas.
Demostramos la proposición cuando los autovalores de ![]() son distintos:
son distintos:
Entonces, podemos asegurar que ![]() es estrictamente
diagonalizable y por tanto, existen tres autovectores
es estrictamente
diagonalizable y por tanto, existen tres autovectores ![]() ortogonales entre sí.
ortogonales entre sí.
Por tanto, ![]() forman una base y
cualquier matriz
forman una base y
cualquier matriz ![]() de
de ![]() se puede expresar como
se puede expresar como
![]() , donde
, donde ![]() siendo
siendo ![]() la forma canónica de
la forma canónica de ![]() .
.
Así que ![]() . Ahora es fácil demostrar que
. Ahora es fácil demostrar que ![]() tiene que ser
simétrica ya que si
tiene que ser
simétrica ya que si
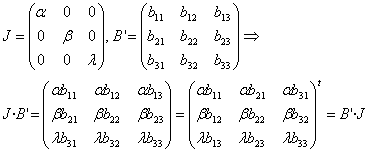
Entonces igualando elementos nos queda ![]() , y como
, y como ![]() (autovalores
distintos), ha de ser
(autovalores
distintos), ha de ser ![]() . De forma análoga llegamos a que
. De forma análoga llegamos a que ![]() para todo
para todo ![]() . Entonces
. Entonces ![]() es diagonal, y por
tanto simétrica.
es diagonal, y por
tanto simétrica.
Ya sólo queda demostrar que ![]() es también simétrica.
Como
es también simétrica.
Como ![]() son ortogonales entre
sí y se pueden tomar de norma 1,
son ortogonales entre
sí y se pueden tomar de norma 1,![]() , por lo que
, por lo que ![]() es simétrica al serlo
es simétrica al serlo ![]() .
.
20.- Compara
![]() y
y ![]() para todo
para todo ![]()
(2006-Segundo día, Problema 3)
Solución
Vamos a ver que ![]() para todo
para todo ![]() . Es claro que
. Es claro que
![]() , para todo
, para todo ![]() , ya que, si
, ya que, si ![]() , entonces
, entonces ![]() (la función
(la función ![]() es estrictamente
creciente en el primer cuadrante), por lo que
es estrictamente
creciente en el primer cuadrante), por lo que ![]() (
(![]() es estrictamente creciente en su dominio), por lo que basta
con ver que
es estrictamente creciente en su dominio), por lo que basta
con ver que ![]() para todo
para todo ![]() .
.
Para ello, vemos que ![]() para todo
para todo ![]() . Para ello, desarrollamos por Taylor en el 0 la función de
la izquierda: Si llamamos
. Para ello, desarrollamos por Taylor en el 0 la función de
la izquierda: Si llamamos ![]() , tenemos que
, tenemos que ![]() , siendo sus sucesivas derivadas en el 0:
, siendo sus sucesivas derivadas en el 0:
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Por tanto, ![]()
Se cumple entonces que

(Donde los puntos suspensivos indican términos de mayor
grado). Por tanto, ![]() para todo
para todo ![]() , para cierto número
, para cierto número ![]() (se cumple que
(se cumple que
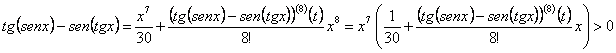 si
si ![]() y
y ![]() está cerca de 0, ya
que
está cerca de 0, ya
que ![]() si
si ![]() , al ser
, al ser ![]() continua y
continua y ![]() ). Para ver que la función es positiva en todo el intervalo que
nos piden, hacemos lo siguiente:
). Para ver que la función es positiva en todo el intervalo que
nos piden, hacemos lo siguiente:
![]() (Ya que si
(Ya que si ![]() , se cumple que
, se cumple que ![]() , por lo que
, por lo que ![]() ).
).
Por tanto, si llamamos ![]() , hay que ver que
, hay que ver que ![]() para todo
para todo ![]() (sabemos por lo
anterior que
(sabemos por lo
anterior que ![]() para todo
para todo ![]() , para cierto número
, para cierto número ![]() ).
).
Para ello, vemos el signo de ![]() en las raíces de
en las raíces de ![]() en
en ![]() , si existen:
, si existen:

Entonces se cumple que:
![]() . Es decir, en los puntos donde
. Es decir, en los puntos donde ![]() , si existen,
, si existen, ![]() tiene el mismo signo
que
tiene el mismo signo
que
![]() . Para ver el signo de
. Para ver el signo de ![]() en
en ![]() , vemos el signo de
, vemos el signo de ![]() en las raíces de
en las raíces de ![]() en
en ![]() , si existen:
, si existen:
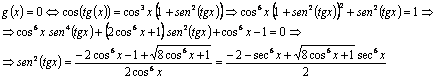
(Tomamos sólo la raíz positiva porque ![]() ).
).
Entonces, ![]() (tomamos sólo la raíz
positiva porque
(tomamos sólo la raíz
positiva porque 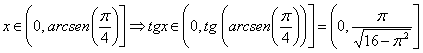 , por lo que
, por lo que ![]() al ser
al ser ![]() , ya que
, ya que ![]() . La raíz está definida al ser
. La raíz está definida al ser ![]() , ya que
, ya que ![]() , al ser
, al ser ![]() ). Por tanto,
). Por tanto,
![]()
Entonces donde ![]() ,
,
 , y esta última función tiene el mismo signo que
, y esta última función tiene el mismo signo que
![]() .
.
Vamos a ver que
![]() , para todo
, para todo![]() :
:


Y esto último es equivalente con
![]()
Si hacemos ahora el cambio de variable ![]() tenemos que, como
tenemos que, como ![]() ,
, 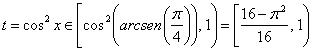 .
.
Por tanto, la desigualdad anterior queda
![]() . Se puede ver por la regla de Ruffini que
el polinomio de la izquierda tiene la raíz
. Se puede ver por la regla de Ruffini que
el polinomio de la izquierda tiene la raíz ![]() triple, luego la
desigualdad se factoriza como
triple, luego la
desigualdad se factoriza como ![]() .
.
Como ![]() , tenemos que
, tenemos que ![]() , luego para demostrar la desigualdad deseada basta ver que
, luego para demostrar la desigualdad deseada basta ver que ![]() , si
, si 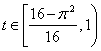 .
.
Para ver esto, observamos que ![]() tiene el mismo signo
que
tiene el mismo signo
que ![]() ,
, ![]() tiene el mismo signo
que
tiene el mismo signo
que ![]() ,
, ![]() tiene el mismo signo
que
tiene el mismo signo
que ![]() , y
, y ![]() tiene el mismo signo
que
tiene el mismo signo
que ![]() . Hallamos las raíces de este último polinomio:
. Hallamos las raíces de este último polinomio:
![]() , por lo que, al ser el coeficiente de
, por lo que, al ser el coeficiente de ![]() positivo, tenemos que
positivo, tenemos que ![]() para todo
para todo ![]() , y entonces
, y entonces ![]() es estrictamente
creciente, con
es estrictamente
creciente, con ![]() , por lo que
, por lo que ![]() si
si ![]() , y entonces
, y entonces ![]() es estrictamente
creciente en ese intervalo, con
es estrictamente
creciente en ese intervalo, con ![]() , por lo que
, por lo que ![]() si
si ![]() , y entonces
, y entonces ![]() es estrictamente
creciente en ese intervalo, con
es estrictamente
creciente en ese intervalo, con ![]() , por lo que
, por lo que ![]() si
si ![]() , y entonces
, y entonces ![]() es estrictamente
creciente en ese intervalo, con
es estrictamente
creciente en ese intervalo, con ![]() , por lo que
, por lo que ![]() si
si ![]() , y en concreto
, y en concreto ![]() si
si 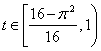 , como queríamos. Por tanto tenemos que
, como queríamos. Por tanto tenemos que ![]() para todo
para todo ![]() , y entonces
, y entonces ![]() donde
donde ![]() , si
, si ![]() .
.
Vamos a ver que esto implica que ![]() no tiene raíces en
este intervalo. Para ello, hallamos ahora el polinomio de Taylor de
no tiene raíces en
este intervalo. Para ello, hallamos ahora el polinomio de Taylor de ![]() en 0: se cumple que
en 0: se cumple que
![]()

Por lo que:
![]()
Por otro lado,
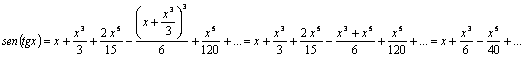
Entonces:
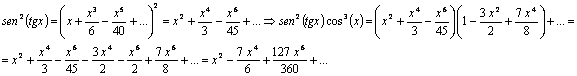
Por tanto,
![]() , lo que implica que
, lo que implica que ![]() si
si ![]() para cierto número
para cierto número ![]() , al ser
, al ser ![]() si
si ![]() . Esto indica que
. Esto indica que ![]() no tiene ninguna raíz
en
no tiene ninguna raíz
en ![]() , ya que si tuviera alguna, estaría en
, ya que si tuviera alguna, estaría en ![]() , por lo que habría un mínimo de las raíces de
, por lo que habría un mínimo de las raíces de ![]() en ese intervalo,
llamémosle
en ese intervalo,
llamémosle ![]() , pero como
, pero como ![]() (
(![]() ),
),![]() será estrictamente creciente cerca de
será estrictamente creciente cerca de ![]() , por lo que existe un
, por lo que existe un ![]() tal que
tal que ![]() , y al ser
, y al ser ![]() si
si ![]() , por Bolzano existe un
, por Bolzano existe un ![]() con
con ![]() tal que
tal que ![]() , contradicción con que
, contradicción con que ![]() era la mínima raíz en
era la mínima raíz en ![]() . Por tanto, al ser
. Por tanto, al ser ![]() continua, se cumple
que
continua, se cumple
que ![]() en
en ![]() , por lo que
, por lo que ![]() donde
donde ![]() en
en ![]() , y como
, y como ![]() si
si ![]() para cierto
para cierto ![]() , como vimos al principio, se cumple que
, como vimos al principio, se cumple que ![]() para todo
para todo ![]() , como queríamos (repitiendo el argumento visto para
, como queríamos (repitiendo el argumento visto para ![]() )
)