3. 4.- Otros problemas
21.- Evaluar 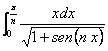 , donde n
es un entero positivo.
, donde n
es un entero positivo.
(Propuesto por José Luís
Díaz Barrero)
Solución
Aplicando el cambio de variable ![]() , tenemos:
, tenemos:
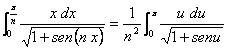 , así que tenemos que resolver la segunda que no depende de n.
, así que tenemos que resolver la segunda que no depende de n.
Para hacer la segunda integral,
hacemos primero ![]() . Para ello, hacemos el cambio de variable
. Para ello, hacemos el cambio de variable ![]() , por lo que
, por lo que
![]()
(como ![]() ,
, ![]() , por lo que
, por lo que ![]() , y entonces
, y entonces ![]() ).
).
Si hacemos ahora el cambio ![]() , tenemos que
, tenemos que 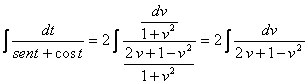 .
.
Las raíces de ![]() son
son ![]() , por lo que el denominador se descompone como
, por lo que el denominador se descompone como ![]() , y entonces
, y entonces
![]()
Dando el valor ![]() , tenemos
, tenemos ![]() , dando el valor
, dando el valor ![]() , tenemos
, tenemos ![]() , por lo que
, por lo que ![]() , y entonces
, y entonces
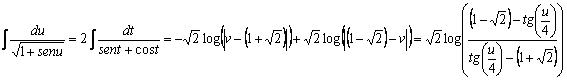 (ya que, como
(ya que, como ![]() ,
, ![]() , por lo que el numerador y el denominador son negativos y
entonces el cociente es positivo, por lo que se puede quitar el valor absoluto).
, por lo que el numerador y el denominador son negativos y
entonces el cociente es positivo, por lo que se puede quitar el valor absoluto).
Entonces, integrando por partes tenemos que
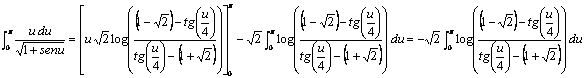
Para hallar esta última integral,
llamamos 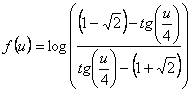 y comprobamos que, si
ponemos el origen de coordenadas en el punto medio del intervalo, es decir, en
y comprobamos que, si
ponemos el origen de coordenadas en el punto medio del intervalo, es decir, en ![]() ,
, ![]() es impar ó, lo que es
lo mismo,
es impar ó, lo que es
lo mismo,
![]() .
.
Esto implica que ![]() , por lo que
, por lo que

Y entonces 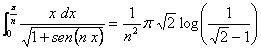
(La tercera igualdad es porque 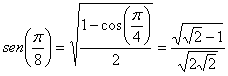 ,
, 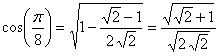 , por lo que
, por lo que 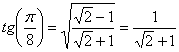 )
)
Para comprobar la igualdad ![]() , nos fijamos en que
, nos fijamos en que ![]() como vimos antes, por
lo que
como vimos antes, por
lo que
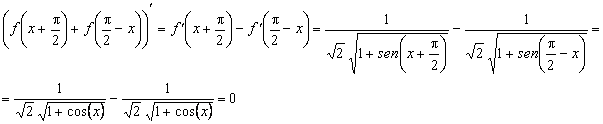
y entonces ![]() . Valorando en
. Valorando en ![]() , tenemos que
, tenemos que ![]() , por lo que
, por lo que ![]() .
.
Observaciones
1) ![]() es el valor medio del
teorema de la media de
es el valor medio del
teorema de la media de ![]() en
en ![]() si
si ![]() cumple la condición
anterior y es continua.
cumple la condición
anterior y es continua.
2) En general, se cumple que ![]() si
si ![]() cumple la condición
anterior y es continua, ya que
cumple la condición
anterior y es continua, ya que
![]() , por lo que
, por lo que ![]() , y sustituyendo
, y sustituyendo ![]() por 0 tenemos
por 0 tenemos ![]() , y entonces
, y entonces ![]() .
.
3) Más en general, si una función
continua ![]() cumple que
cumple que
![]() , para ciertos
, para ciertos ![]() , para todo
, para todo ![]() , entonces se cumple que
, entonces se cumple que ![]() :
: ![]() es el valor promedio
integral, si
es el valor promedio
integral, si ![]()
22.- Demostrar que 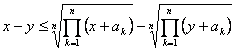 para
para ![]() , con
, con ![]()
Solución
Como ![]() es un polinomio
genérico mónico de grado
es un polinomio
genérico mónico de grado ![]() con raíces
negativas, el enunciado es equivalente a probar que:
con raíces
negativas, el enunciado es equivalente a probar que:
![]() , siendo
, siendo ![]() un polinomio mónico de grado
un polinomio mónico de grado ![]() con raíces negativas
con raíces negativas ![]() ,
, ![]()
Aplicamos inducción respecto ![]() : Para
: Para ![]() , se cumple que
, se cumple que ![]() , y entonces
, y entonces ![]()
Supongamos que el resultado es verdad para
grado ![]() , sea
, sea ![]() , definida en el dominio:
, definida en el dominio:
![]() . (La función
. (La función ![]() está bien definida en
está bien definida en ![]() , ya que
, ya que ![]() para
para ![]() ).
).
Vamos a evaluar ![]() en sus puntos
críticos:
en sus puntos
críticos:
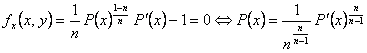 ,
,
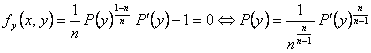 , así que en los puntos críticos de
, así que en los puntos críticos de ![]() en
en ![]() , si hay, tenemos que
, si hay, tenemos que
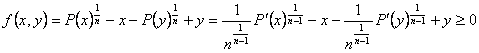
(Inducción: ![]() es un polinomio mónico de grado
es un polinomio mónico de grado ![]() con raíces
negativas
con raíces
negativas ![]() , dado que
, dado que ![]() tiene raíces
negativas, y, para
tiene raíces
negativas, y, para ![]() , tenemos que
, tenemos que
![]() , porque
, porque ![]() : las raíces de
: las raíces de ![]() están entre las raíces
de
están entre las raíces
de ![]() )
)
En la frontera ![]() , tenemos
, tenemos ![]() . En la frontera
. En la frontera ![]() , tenemos que
, tenemos que ![]() , y entonces
, y entonces
![]()
Además,
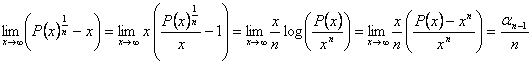
Por lo que tenemos que
![]()
Luego ![]() tiene mínimo 0 en
tiene mínimo 0 en ![]() , por lo que
, por lo que ![]() para
para ![]()
Observación
Como no hemos usado en ningún
momento que ![]() sean positivos,
tenemos el siguiente enunciado paralelo al inicial, más general:
sean positivos,
tenemos el siguiente enunciado paralelo al inicial, más general:
Sea ![]() un polinomio mónico de grado
un polinomio mónico de grado ![]() con raíces reales
con raíces reales ![]() , entonces
, entonces ![]() , para
, para ![]()
23.- Sea ![]() un polinomio mónico de grado
un polinomio mónico de grado ![]() con raíces reales
con raíces reales ![]() , probar que
, probar que ![]() para
para ![]()
Solución
En el problema anterior hemos visto
que ![]() para
para
![]() , lo que implica que la función
, lo que implica que la función ![]() es creciente en
es creciente en ![]() , y entonces
, y entonces ![]() , por lo que
, por lo que ![]() , y entonces
, y entonces ![]() (por lo que el primer
coeficiente del polinomio
(por lo que el primer
coeficiente del polinomio ![]() es negativo si este
polinomio no es el polinomio nulo)
es negativo si este
polinomio no es el polinomio nulo)
Observaciones
1) Como
consecuencia de este problema, un polinomio ![]() , con raíces negativas
, con raíces negativas
![]() ,
,
debe satisfacer ![]() , es decir,
, es decir, ![]() . Un polinomio que no satisface esta desigualdad debe tener
alguna raíz no negativa.
. Un polinomio que no satisface esta desigualdad debe tener
alguna raíz no negativa.
2) La
desigualdad de la observación 1 lleva a ![]() , para
, para ![]()
3) El recíproco
de la observación 1 no es verdad, dado que ![]() satisface
satisface ![]() , pero tiene la raíz positiva 1.
, pero tiene la raíz positiva 1.
4) Como otra
consecuencia del problema, si ![]() para
para ![]() grande (si el
coeficiente del primer término del polinomio
grande (si el
coeficiente del primer término del polinomio ![]() es positivo), entonces
es positivo), entonces
![]() tiene alguna raíz no
real. Esto ocurre con
tiene alguna raíz no
real. Esto ocurre con ![]() , para el que
, para el que ![]()
5) El recíproco
de 4 tampoco es verdad, dado que ![]() , tiene las raíces no reales
, tiene las raíces no reales ![]() , pero no satisface
, pero no satisface 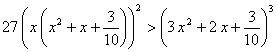 para
para ![]() grande (el primer
coeficiente de
grande (el primer
coeficiente de 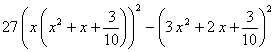 es
es ![]() , negativo).
, negativo).
24.- Para todos los enteros ![]() ,
, ![]() (
(![]() positivo), determinar
positivo), determinar 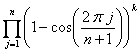
(Propuesto por José Luís Díaz Barrero)
Solución
Tenemos que ![]() , luego
, luego 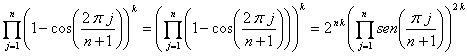
Para
evaluar ![]() , observamos que, para
, observamos que, para ![]() par y
par y ![]() ,
,

Entonces, como ![]() (
(![]() ), tenemos que
), tenemos que ![]() ,
, ![]() , es raíz del polinomio
, es raíz del polinomio ![]()
Dado que ![]() es una función par,
las otras raíces del polinomio son
es una función par,
las otras raíces del polinomio son ![]() , con
, con ![]() , luego tenemos que
, luego tenemos que

Esto implica que
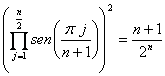 , dado que
, dado que ![]() : sabemos que
: sabemos que
![]() ,
, ![]()
Luego sumando
las dos igualdades, obtenemos 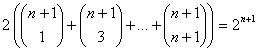 , y entonces
, y entonces ![]()
Ahora, para ![]() tenemos que
tenemos que ![]() , con
, con ![]() , luego
, luego
 , y entonces
, y entonces 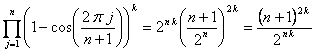
Para ![]() impar y
impar y ![]() ,
,
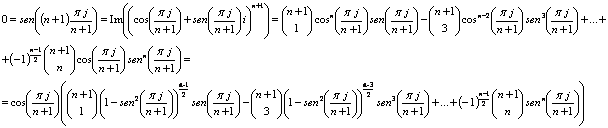
Como ![]() ,
, ![]() (
(![]() ), tenemos que
), tenemos que ![]() ,
, ![]() , es raíz del polinomio
, es raíz del polinomio
![]()
Dado que ![]() es una función par,
las otras raíces del polinomio son
es una función par,
las otras raíces del polinomio son ![]() ,
, ![]() , por lo que
, por lo que

Esto implica que
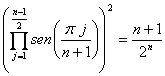 .
.
Ahora, como 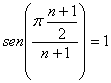 y, para
y, para ![]() , tenemos que
, tenemos que ![]() ,
,
con ![]() , también en este caso:
, también en este caso:
 , y entonces
, y entonces 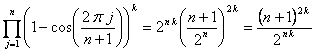
Observación
Sustituyendo ![]() por
por ![]() en la expresión
de
en la expresión
de  , obtenemos
, obtenemos 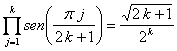 , sustituyendo
, sustituyendo ![]() por
por ![]() en la expresión
de
en la expresión
de
 , obtenemos
, obtenemos 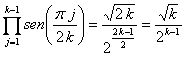
25.- Evalúa ![]() para
para ![]() par
par
Solución
Vemos primero la
relación entre ![]() ,
, ![]() para
para ![]() par:
par:
Si ![]() ,
, ![]() toma todos los números
pares de
toma todos los números
pares de ![]() . Si
. Si ![]() ,
, ![]() ,
,
donde ![]() toma todos los números
impares desde
toma todos los números
impares desde ![]() hasta
hasta ![]() , luego
, luego ![]()
Ahora, tenemos que:
![]() , por lo que
, por lo que ![]()
(Es claro que
para n impar ![]() , ya que para
, ya que para ![]() ,
, 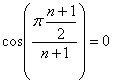 )
)
Observaciones
1) Para obtener ![]() , observamos que, para
, observamos que, para ![]() ,
, ![]() , con
, con ![]() , luego
, luego
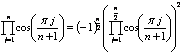 , y entonces
, y entonces  , luego cambiando
, luego cambiando ![]() por
por ![]() , obtenemos
, obtenemos ![]()
2) Para obtener ![]() , vemos que
, vemos que

Por tanto, ![]() (¡Igual que
(¡Igual que ![]() !)
!)
En la primera
igualdad hemos aplicado la expresión ![]() para
para ![]() , que se obtenía en la observación al problema anterior, y en
la última, la expresión que se obtenía en la solución del problema anterior
para
, que se obtenía en la observación al problema anterior, y en
la última, la expresión que se obtenía en la solución del problema anterior
para ![]() , cambiando
, cambiando ![]() por
por ![]()
26.- Supongamos que el polinomio ![]() puede ser factorizado
como
puede ser factorizado
como ![]() , donde
, donde ![]() son números reales
positivos,
son números reales
positivos, ![]() es un número par.
Prueba que
es un número par.
Prueba que ![]()
(Propuesto por José Luís Díaz Barrero)
Solución
Como ![]() es un número par, el
enunciado es equivalente a
es un número par, el
enunciado es equivalente a
![]() , para números positivos
, para números positivos ![]() .
.
Si llamamos ![]() (el subíndice es
porque tenemos
(el subíndice es
porque tenemos ![]() números positivos), la
desigualdad es
números positivos), la
desigualdad es
![]() . Vamos a probar por inducción que esta desigualdad es cierta
para todo
. Vamos a probar por inducción que esta desigualdad es cierta
para todo ![]() :
:
Para ![]() , tenemos que
, tenemos que ![]() , y esta última desigualdad es cierta (de hecho, el resultado
es verdad en el caso
, y esta última desigualdad es cierta (de hecho, el resultado
es verdad en el caso ![]() para todos los números
reales
para todos los números
reales ![]() . La igualdad se verifica si y solo si
. La igualdad se verifica si y solo si ![]() ).
).
Supongamos que
el resultado es verdad para ![]() , para
, para ![]() podemos reescribir la
desigualdad como
podemos reescribir la
desigualdad como
![]()
Como ![]() son números positivos,
son números positivos,
![]() es
es ![]() , luego la desigualdad queda
, luego la desigualdad queda
![]() . El lado izquierdo de la
desigualdad es un polinomio de segundo grado en
. El lado izquierdo de la
desigualdad es un polinomio de segundo grado en ![]() , llamémosle
, llamémosle ![]() , por tanto una parábola. Si la coordenada
, por tanto una parábola. Si la coordenada ![]() de su vértice
es
de su vértice
es ![]() , es decir, si
, es decir, si ![]() , entonces la desigualdad
, entonces la desigualdad ![]() se verifica para
se verifica para ![]() , dado que
, dado que ![]() es estrictamente
creciente en
es estrictamente
creciente en ![]() (el coeficiente
de
(el coeficiente
de ![]() es
es ![]() ), y
), y ![]()
La condición ![]() se verifica si
se verifica si ![]() . Si la coordenada
. Si la coordenada ![]() del vértice es
del vértice es ![]() , es decir, si
, es decir, si ![]() , tenemos que ver que
, tenemos que ver que ![]() no tiene dos raíces
reales distintas, lo que implica que
no tiene dos raíces
reales distintas, lo que implica que ![]() para todo número
real
para todo número
real ![]() . Por tanto, tenemos que ver que el discriminante es
. Por tanto, tenemos que ver que el discriminante es ![]() :
:
![]() . Y esto se cumple si:
. Y esto se cumple si:
![]()
Pero la primera
desigualdad es cierta (inducción), y la segunda también dado que ![]()
Observaciones
1) Para ![]() impar, tenemos
que
impar, tenemos
que
![]() ,
, ![]() . Por tanto, como hemos visto que
. Por tanto, como hemos visto que
![]() para todo
para todo ![]() , tenemos la siguiente afirmación análoga a la
inicial:
, tenemos la siguiente afirmación análoga a la
inicial:
Supongamos que
el polinomio ![]() puede ser factorizado como
puede ser factorizado como ![]() , donde
, donde ![]() son números reales
positivos,
son números reales
positivos, ![]() es un número impar.
Entonces
es un número impar.
Entonces ![]()
2) Vemos que la
igualdad en estas afirmaciones se verifica si y sólo si ![]() . Para verlo, probamos que la igualdad en
. Para verlo, probamos que la igualdad en
![]() , se verifica si y sólo si
, se verifica si y sólo si ![]() , para todo
, para todo ![]() . Aplicamos inducción respecto a
. Aplicamos inducción respecto a ![]() :
:
Para ![]() , lo vimos en la resolución del problema.
, lo vimos en la resolución del problema.
Supongamos que el
resultado es cierto para ![]() . Para
. Para ![]() , como se ve en la solución del problema, la única
forma de obtener la igualdad es si
, como se ve en la solución del problema, la única
forma de obtener la igualdad es si
![]() .
.
Esto sólo pasa
si ![]() (lo que no puede ser, ya
que vimos que
(lo que no puede ser, ya
que vimos que ![]() ), ó si
), ó si ![]() .
.
Pero por
inducción, esta última igualdad se verifica si y sólo si ![]() , y entonces la igualdad inicial queda:
, y entonces la igualdad inicial queda:
![]() , con solución:
, con solución:
![]() , y entonces
, y entonces ![]()
27.- Encontrar el máximo común divisor de
los números ![]() ,
, ![]() , …,
, …, ![]()
(Propuesto por José Luís Díaz Barrero)
Solución
Vemos primero
que, si un número primo ![]() divide a
divide a ![]() ,
, ![]() , …,
, …, ![]() , entonces divide a
, entonces divide a ![]() luego
luego ![]() . (La igualdad
. (La igualdad ![]() fue probada en la solución
al problema 24)
fue probada en la solución
al problema 24)
Si expresamos
ahora ![]() como
como ![]() , podemos ver que
, podemos ver que ![]() divide a
divide a ![]() para
para ![]() :
:
Como ![]() divide a
divide a ![]() , basta con probar que la potencia de 2 en
, basta con probar que la potencia de 2 en ![]() es mayor ó igual que
la potencia de 2 en
es mayor ó igual que
la potencia de 2 en ![]() .
.
Pero como las potencias de 2 las dan los factores
pares, tenemos que la potencia de 2 en ![]() es igual a la potencia
de 2 en
es igual a la potencia
de 2 en
![]() y la potencia de 2
en
y la potencia de 2
en ![]() es igual a la potencia
de 2 en
es igual a la potencia
de 2 en ![]() . Entonces, si simplificamos por
. Entonces, si simplificamos por ![]() , tenemos que lo que hay que probar es que la potencia
de 2 en
, tenemos que lo que hay que probar es que la potencia
de 2 en ![]() es mayor ó igual que
la potencia de 2 en
es mayor ó igual que
la potencia de 2 en ![]() .
.
Pero, como ![]() , tenemos que
, tenemos que ![]() , luego
, luego ![]() divide a
divide a ![]() , y entonces la potencia de 2 en
, y entonces la potencia de 2 en ![]() es mayor ó igual que
la potencia de 2 en
es mayor ó igual que
la potencia de 2 en ![]() .
.
Pero, para ![]() , tenemos que
, tenemos que ![]() no divide a
no divide a ![]() , luego el máximo común divisor de
, luego el máximo común divisor de ![]() ,
, ![]() , …,
, …, ![]() es
es ![]()
Observación
Se sabe que ![]() divide a
divide a ![]() (
(![]() es el máximo común divisor de
es el máximo común divisor de ![]() ). Eligiendo
). Eligiendo ![]() , este
resultado implica el que hemos demostrado en la solución: Si
, este
resultado implica el que hemos demostrado en la solución: Si ![]() divide a
divide a ![]() , entonces divide a
, entonces divide a ![]()
28.- Encontrar una fórmula para la potencia de 2 en la descomposición en
factores primos de ![]() (
(![]() ) y para la potencia de 2 en la descomposición en factores
primos de
) y para la potencia de 2 en la descomposición en factores
primos de ![]()
Solución
Primero
encontramos una fórmula para la potencia de 2 en la descomposición en factores
primos de ![]() :
:
Los factores
pares de ![]() son de la forma:
son de la forma: ![]() , con
, con ![]() , donde
, donde ![]() es la parte entera (ya
que
es la parte entera (ya
que ![]() ). Estos aportan
). Estos aportan ![]() al exponente de 2 en
la descomposición en factores primos de
al exponente de 2 en
la descomposición en factores primos de ![]()
Contamos cuántos
factores hay de este tipo para un ![]() fijo:
fijo:
Como ![]() , tenemos que
, tenemos que 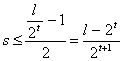 , por lo que
, por lo que  , y entonces el número de factores es
, y entonces el número de factores es 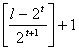
Por tanto, la
potencia de 2 en ![]() es
es 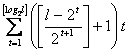
Buscamos ahora
una fórmula para la potencia de 2 en ![]() :
:
Los factores
pares de ![]() son de la forma:
son de la forma: ![]() , con
, con ![]() (ya que
(ya que ![]() ). Estos aportan
). Estos aportan ![]() al exponente de 2 en
la descomposición en factores primos de
al exponente de 2 en
la descomposición en factores primos de ![]()
Contamos cuántos
factores hay de este tipo para un ![]() fijo:
fijo:
Como ![]() , tenemos que
, tenemos que 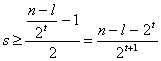 , por lo que
, por lo que
 si
si ![]() ,
, 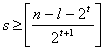 si
si ![]() .
.
Esta última
condición sólo ocurre cuando ![]() , es decir, cuando
, es decir, cuando ![]() , para
, para ![]()
Como ![]() , tenemos que
, tenemos que 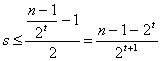 , luego
, luego 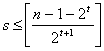 , y entonces el número de factores es
, y entonces el número de factores es
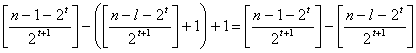 , si 2 no divide a
, si 2 no divide a ![]() ,
, 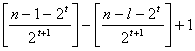 si
si ![]()
Por tanto, la
potencia de 2 en ![]() es
es
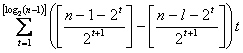 , si 2 no divide a
, si 2 no divide a ![]() ,
, 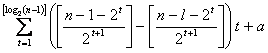 , si
, si ![]()
Observación
Como ![]() divide a
divide a ![]() como vimos antes,
tenemos que, para todo
como vimos antes,
tenemos que, para todo ![]() , con
, con ![]() , se cumple que
, se cumple que
 , donde
, donde ![]() es el exponente
de 2 en la descomposición en factores primos de
es el exponente
de 2 en la descomposición en factores primos de ![]()
29.- Sea n un entero positivo.
Prueba la desigualdad 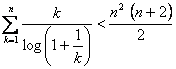
(Propuesto por José Luís Díaz Barrero)
Solución
Aplicamos
inducción respecto a n: para n=1, la desigualdad es ![]() , luego es verdad.
, luego es verdad.
Supongamos
que es cierta para n, para n+1 tenemos 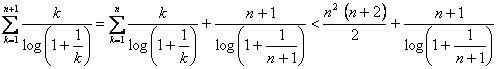 (hemos aplicado la
hipótesis de inducción en la desigualdad), luego acabamos si probamos que
(hemos aplicado la
hipótesis de inducción en la desigualdad), luego acabamos si probamos que 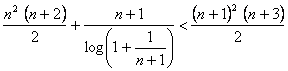 , ó lo que es lo mismo:
, ó lo que es lo mismo:
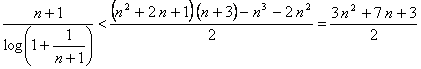 , es decir,
, es decir, ![]() .
.
Por tanto, si
consideramos la función real ![]() , basta con probar que
, basta con probar que ![]() si x≥1 para probar la anterior
desigualdad.
si x≥1 para probar la anterior
desigualdad.
Pero tenemos que
![]()
El denominador
de esta última expresión es positivo si x≥1.
Desarrollando el numerador, obtenemos ![]() .
.
Vamos a ver que ![]() si x≥1:
si x≥1:
Se cumple que ![]() si x≥1, luego P es estrictamente decreciente cuando x≥1, siendo
si x≥1, luego P es estrictamente decreciente cuando x≥1, siendo ![]() , luego
, luego ![]() para x≥1. Por tanto,
para x≥1. Por tanto, ![]() si x≥1, luego f es estrictamente decreciente cuando x≥1, y
si x≥1, luego f es estrictamente decreciente cuando x≥1, y ![]() . Esto implica que
. Esto implica que
![]() si x≥1, como deseábamos.
si x≥1, como deseábamos.
30.- Sea ![]() , y sea
, y sea ![]() una función tal
que
una función tal
que ![]() y
y ![]() es acotada en
es acotada en ![]() . Sea la sucesión
. Sea la sucesión  , determinar su límite.
, determinar su límite.
(Propuesto por José Luís Díaz Barrero)
Solución
Aplicando el teorema de Taylor a ![]() en
en ![]() , con
, con ![]() (
(![]() ), obtenemos
que
), obtenemos
que ![]() , con
, con ![]() . Entonces tenemos que
. Entonces tenemos que
![]() , donde
, donde ![]() es una cota superior de
es una cota superior de ![]() .
.
Por tanto,
para ![]() tenemos que
tenemos que ![]() , es decir:
, es decir:
![]()
Pero como ![]() , tenemos que
, tenemos que ![]() cuando
cuando ![]() , por lo que las cotas inferiores y superiores de
, por lo que las cotas inferiores y superiores de ![]() halladas tienden a
halladas tienden a ![]() , y entonces
, y entonces ![]() (regla
de Sandwich).
(regla
de Sandwich).