3. 4.- Otros problemas
11.- Encontrar todas las funciones ![]() tales que
tales que
![]()
(OME-fase
local, 2005)
Solución
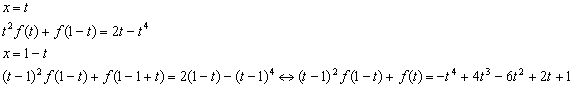
Tenemos dos ecuaciones con dos
incógnitas ![]() y basta despejar
y basta despejar ![]() para acabar. Resulta
para acabar. Resulta ![]()
12.- Sea ![]() un entero no negativo.
Demostrar que la ecuación
un entero no negativo.
Demostrar que la ecuación
![]()
tiene solo soluciones enteras y
determinarlas. (![]() representa el n-ésimo número de
Fibonacci, definido por
representa el n-ésimo número de
Fibonacci, definido por ![]() ,
, ![]() y, para
y, para ![]() ,
, ![]() )
)
(Propuesto por José Luís Díaz Barrero)
Solución
Los divisores de ![]() son posibles soluciones enteras de la
ecuación. Si probamos con
son posibles soluciones enteras de la
ecuación. Si probamos con ![]() ,
obtenemos que es una solución de la ecuación, y es entera dado que
,
obtenemos que es una solución de la ecuación, y es entera dado que ![]() es entero para todo
es entero para todo ![]() como se puede ver
fácilmente por inducción. Además, la parte izquierda de la ecuación se
factoriza como:
como se puede ver
fácilmente por inducción. Además, la parte izquierda de la ecuación se
factoriza como:
![]()
Entonces las otras soluciones de la ecuación son las
soluciones de la ecuación bicuadrada ![]() . Si
resolvemos esta última ecuación para los primeros valores de
. Si
resolvemos esta última ecuación para los primeros valores de ![]() , vemos que una de las soluciones positivas parece ser
, vemos que una de las soluciones positivas parece ser ![]() .
Comprobamos que
.
Comprobamos que ![]() es una de las soluciones positivas para todo
es una de las soluciones positivas para todo ![]() .
.
Para ello, obtenemos una expresión explícita para ![]() : La
ecuación de recurrencia
: La
ecuación de recurrencia ![]() tiene como ecuación
característica
tiene como ecuación
característica ![]() , con soluciones
, con soluciones ![]() , así que la solución general de la recurrencia es
, así que la solución general de la recurrencia es 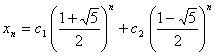 .
. ![]() , es
la única solución de la recurrencia con
, es
la única solución de la recurrencia con ![]() y
y ![]() , por
tanto
, por
tanto 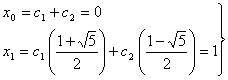 , y
entonces
, y
entonces ![]() y
y ![]() , por lo que
, por lo que 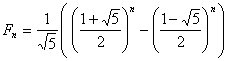
Ahora sustituimos este último valor en la ecuación
bicuadrada:

Entonces, como la ecuación es bicuadrada, se cumple que ![]() ,
, ![]() son dos soluciones enteras de la ecuación.
son dos soluciones enteras de la ecuación.
La otra solución positiva de la ecuación bicuadrada, llamémosla
![]() ,
parece ser la solución de la recurrencia de Fibonacci
,
parece ser la solución de la recurrencia de Fibonacci ![]() , con las condiciones
iniciales
, con las condiciones
iniciales ![]() y
y ![]() . Buscamos una
expresión explícita para
. Buscamos una
expresión explícita para ![]() :
:
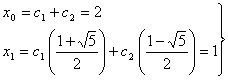 , y
entonces
, y
entonces ![]() y
y ![]() ,
, 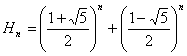
Ahora sustituimos este último valor en la ecuación bicuadrada
para comprobar que ![]() la satisface:
la satisface:

Por tanto, las otras soluciones de la ecuación son ![]() y
y ![]() , que
son enteras dado que
, que
son enteras dado que ![]() es entera, como puede verse fácilmente por
inducción.
es entera, como puede verse fácilmente por
inducción.
Observación
El número ![]() definido en la solución es el conocido como n-ésimo número de Lucas
definido en la solución es el conocido como n-ésimo número de Lucas
13.- Determinar para qué valores
enteros del parámetro ![]() existen soluciones
enteras de la ecuación
existen soluciones
enteras de la ecuación ![]()
(Propuesto
en La
Gaceta de la R. S. M. E.- Problema 66)
Solución
La ecuación se puede escribir como ![]() , ecuación de
Fermat de grado 3, luego sólo tiene las soluciones enteras triviales
, ecuación de
Fermat de grado 3, luego sólo tiene las soluciones enteras triviales ![]() y
y ![]() , imposible, ó
, imposible, ó ![]() y
y ![]() , luego
, luego ![]() es el único valor
entero para el que la ecuación tiene solución entera.
es el único valor
entero para el que la ecuación tiene solución entera.
Observación
No se puede dar la solución trivial ![]() , ya que entonces
, ya que entonces ![]() . Se dará esta solución racional para
. Se dará esta solución racional para ![]() , valor hallado antes;
, valor hallado antes; ![]() es por tanto el único
valor racional para el que la ecuación tiene solución racional.
es por tanto el único
valor racional para el que la ecuación tiene solución racional.
14.- Resolver en los enteros
positivos la ecuación ![]()
(Propuesto
en
Solución
La ecuación es equivalente a ![]() , luego una solución con
, luego una solución con ![]() naturales es una forma
de expresar 15 como el producto de 2 números naturales, ya que si
naturales es una forma
de expresar 15 como el producto de 2 números naturales, ya que si ![]() , tenemos que
, tenemos que ![]() y
y ![]() , por lo que, al ser el producto positivo, se cumple que
, por lo que, al ser el producto positivo, se cumple que ![]() .
.
Como ![]() , será
, será ![]() , luego las únicas opciones son:
, luego las únicas opciones son:
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Observaciones
1) Como la ecuación también es equivalente a ![]() , el resultado nos dice que sólo hay 2 valores de
, el resultado nos dice que sólo hay 2 valores de ![]() tales que
tales que ![]() divida a
divida a ![]() , que son
, que son ![]() , para el que los 2 polinomios valen 5, y
, para el que los 2 polinomios valen 5, y ![]() , para el que el primer polinomio vale 15 y el segundo 60
, para el que el primer polinomio vale 15 y el segundo 60
2) Si buscamos todas las soluciones enteras a la ecuación,
tendríamos también:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
15.- Probar que, si ![]() es convergente y existe
es convergente y existe ![]() , entonces
, entonces ![]()
Solución
Si ![]() ,
entonces para
,
entonces para ![]() suficientemente pequeño tal que
suficientemente pequeño tal que ![]() ,
tenemos que existe un número
,
tenemos que existe un número ![]() tal que, para
tal que, para ![]() , se cumple que
, se cumple que ![]() , y
entonces
, y
entonces ![]() , por
lo que
, por
lo que ![]() ,
contradicción con que
,
contradicción con que ![]() es convergente. De forma análoga
podemos probar que
es convergente. De forma análoga
podemos probar que ![]() no puede ser negativo.
no puede ser negativo.
16.-
Probar ó buscar contraejemplos para las siguientes proposiciones:
a)
Sea ![]() una función
continua y tal que
una función
continua y tal que ![]() en
en ![]() para algún
para algún ![]() , y con
, y con ![]() . Entonces, existe
. Entonces, existe ![]()
b)
Sea ![]() una función
continua y tal que
una función
continua y tal que ![]() en
en ![]() para algún
para algún ![]() , y con
, y con ![]() . Entonces, existe
. Entonces, existe ![]()
c)
Sea ![]() una función derivable y creciente en
una función derivable y creciente en ![]() para algún
para algún ![]() , y con una asíntota horizontal en
, y con una asíntota horizontal en ![]() . Entonces, existe
. Entonces, existe ![]()
d)
Sea ![]() una función
derivable y estrictamente creciente en
una función
derivable y estrictamente creciente en ![]() para algún
para algún ![]() , y con una asíntota horizontal en
, y con una asíntota horizontal en ![]() . Entonces, existe
. Entonces, existe ![]()
Solución
a) Es falso: Si consideramos la
función:
 para
para ![]() ,
, ![]() ,
, ![]() es una función bien
definida,
es una función bien
definida,
dado que los intervalos no se
solapan: ![]() , lo que se cumple para
, lo que se cumple para ![]()
Tenemos también que ![]() y
y ![]() es continua en
es continua en ![]() (
(![]() es "unión
de triángulos" definidos en
es "unión
de triángulos" definidos en ![]() y de altura 1):
y de altura 1):
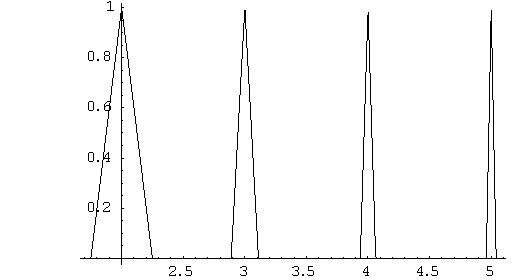 )
)
Además, ![]()
Pero
![]() no existe, dado
que
no existe, dado
que ![]() , y
, y ![]()
b) Es falso: Si consideramos la función:

para ![]() ,
, ![]() , Tenemos que
, Tenemos que ![]() y
y ![]() es continua en
es continua en ![]() , ya que
, ya que ![]() es
"unión" de segmentos uniendo puntos con segunda coordenada positiva:
es
"unión" de segmentos uniendo puntos con segunda coordenada positiva:
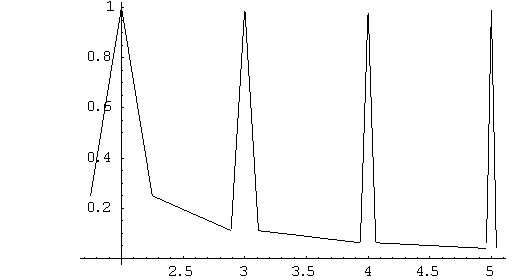
Calculamos las áreas debajo de los
tres segmentos definiendo ![]() :
:
El área debajo del primer ó el
segundo segmento es ![]() , y el área debajo del tercer segmento es
, y el área debajo del tercer segmento es
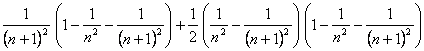 , por lo que
, por lo que
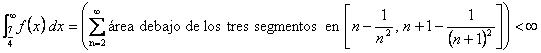 , ya que todos los denominadores tienen grado al menos
dos
, ya que todos los denominadores tienen grado al menos
dos
y los numeradores son constantes.
Pero
![]() no existe, dado que
no existe, dado que ![]() , y
, y ![]()
c) Es falso: Si consideramos la
función ![]() , para la función
, para la función ![]() del apartado
a), tenemos que
del apartado
a), tenemos que ![]() es derivable
dado que
es derivable
dado que ![]() es continua, y
es continua, y ![]() , por lo que
, por lo que ![]() es creciente, y
es creciente, y
![]() , luego
, luego ![]() tiene una
asíntota horizontal en
tiene una
asíntota horizontal en ![]() , pero, al ser
, pero, al ser ![]() , el
, el ![]() no existe.
no existe.
d) Es falso: Si consideramos la
función: ![]() , para la función
, para la función ![]() del apartado
b), tenemos que
del apartado
b), tenemos que ![]() es derivable
dado que
es derivable
dado que ![]() es continua, y
es continua, y ![]() , por lo que
, por lo que ![]() es
estrictamente creciente, y
es
estrictamente creciente, y ![]() , luego
, luego ![]() tiene una
asíntota horizontal en
tiene una
asíntota horizontal en ![]() , pero, al ser
, pero, al ser ![]() , el
, el ![]() no existe.
no existe.
Observación
F se aproxima a la asíntota horizontal con infinitos cambios de convexidad:
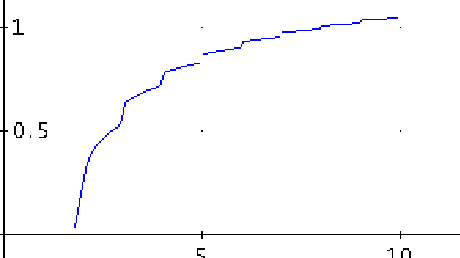
17.-
Sea ![]() una función tal
que
una función tal
que ![]() y
y ![]() . Probar que
. Probar que ![]()
(Propuesto
por José Luís Díaz Barrero)
Solución
Vemos primero que existe una función cumpliendo las condiciones del enunciado.
Para ver esto, definimos primero
inductivamente, para todo ![]() , una función
, una función ![]() en
en ![]() tal que
tal que ![]() para
para ![]() ,
, ![]() si
si ![]() ,
, ![]()
Para
![]() , como
, como ![]() es continua y
Lipschitziana respecto a
es continua y
Lipschitziana respecto a ![]() en
en ![]() (
(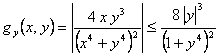 , y esta última función es acotada en R, dado que es continua
y
, y esta última función es acotada en R, dado que es continua
y  ), existe una solución de
), existe una solución de ![]() en
en ![]() tal que
tal que ![]() , por una variación del teorema de
Picard, luego definimos
, por una variación del teorema de
Picard, luego definimos ![]() como esta solución.
como esta solución.
Supongamos que hemos definido ![]() en
en ![]() con las
condiciones requeridas, y consideramos
ahora el problema de Cauchy
con las
condiciones requeridas, y consideramos
ahora el problema de Cauchy ![]() , con
, con ![]() .
.
Como g es también continua y Lipschitziana respecto a ![]() en
en ![]() (
(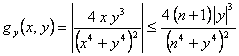 , y esta última función es acotada en R, dado que es continua
y
, y esta última función es acotada en R, dado que es continua
y  ), existe una solución del mencionado problema de Cauchy en
), existe una solución del mencionado problema de Cauchy en ![]() , así que definimos
, así que definimos ![]() como esta solución.
como esta solución.
Entonces podemos definir ![]() como
como ![]() si
si ![]() .
.
Observamos que ![]() está bien definida, ya
que
está bien definida, ya
que ![]() , luego
, luego ![]() es continua en
es continua en ![]() y, para
y, para ![]() , se cumple que
, se cumple que ![]()
Para ![]() tenemos que
tenemos que
![]()
![]() , luego tenemos también que
, luego tenemos también que
![]() , para todo
, para todo ![]() (para
(para ![]() , sólo tenemos que tener en cuenta
, sólo tenemos que tener en cuenta ![]() ). Además, se cumple que
). Además, se cumple que ![]() .
.
Vemos ahora que ![]() tiene límite: Como
tiene límite: Como ![]() para
para ![]() ,
, ![]() es estrictamente
creciente en
es estrictamente
creciente en ![]() , así que
, así que ![]() tiene límite
tiene límite ![]() .
.
Integrando a los 2 lados de la
ecuación inicial, tenemos que, para ![]() ,
,
![]()
(La desigualdad es porque ![]() es una función
creciente, luego
es una función
creciente, luego ![]() para
para ![]() ,
, ![]() para
para ![]() ). Entonces tenemos que
). Entonces tenemos que
![]() .
.
Tomando límites, llegamos a
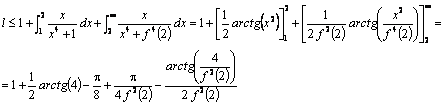
Ahora, consideramos la función  .
.
Vemos que ![]() es estrictamente
decreciente en
es estrictamente
decreciente en ![]() :
:
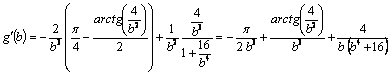 .
.
Estudiar el signo de esta función
para ![]() es equivalente a
estudiar el signo de
es equivalente a
estudiar el signo de ![]() . Tenemos que
. Tenemos que
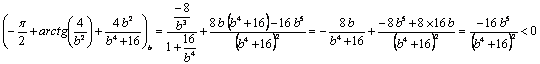 para
para ![]() , luego
, luego ![]() es estrictamente
decreciente y
es estrictamente
decreciente y
![]() , por lo que
, por lo que ![]() para
para ![]() , y entonces
, y entonces ![]() , por lo que
, por lo que ![]() es estrictamente
decreciente en
es estrictamente
decreciente en ![]() , y entonces es estrictamente decreciente en
, y entonces es estrictamente decreciente en ![]() , y entonces, dado que
, y entonces, dado que ![]() , tenemos que
, tenemos que
![]() , por lo que
, por lo que ![]() .
.
18.-
Resolver el problema de Cauchy ![]() ,
, ![]() , para
, para ![]() ,
, ![]() funciones derivables
y positivas en
funciones derivables
y positivas en ![]()
Solución
![]() . Tiene el factor
integrante
. Tiene el factor
integrante ![]() , dado que
, dado que ![]() . Por tanto, la solución general es
. Por tanto, la solución general es ![]() . Para encontrar
. Para encontrar ![]() , vemos que
, vemos que
![]() , luego la solución general queda
, luego la solución general queda ![]() .
.
Como
![]() , tenemos que
, tenemos que ![]() , luego la solución al problema es:
, luego la solución al problema es:
![]()
Observación
En el caso particular ![]() y
y ![]() , la ecuación es similar a la del problema anterior:
, la ecuación es similar a la del problema anterior: ![]() . Según lo visto antes, la solución del problema de Cauchy es
. Según lo visto antes, la solución del problema de Cauchy es
![]() , esto es,
, esto es, ![]()
En este caso, como ![]() para
para ![]() , tenemos que la solución es estrictamente decreciente, y su
límite es
, tenemos que la solución es estrictamente decreciente, y su
límite es ![]() : Si el límite fuera finito, tomando límites en los 2 lados
de la última igualdad cuando
: Si el límite fuera finito, tomando límites en los 2 lados
de la última igualdad cuando ![]() , tendríamos
, tendríamos ![]() , contradicción.
, contradicción.
19.-
Sean ![]() números
complejos. Prueba la desigualdad
números
complejos. Prueba la desigualdad
![]()
(Propuesto
por José Luís Díaz Barrero)
Solución
Llamando ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() y
y
![]() , vemos que la desigualdad es equivalente a
, vemos que la desigualdad es equivalente a
![]() . Pero la parte izquierda de la desigualdad es:
. Pero la parte izquierda de la desigualdad es:
![]() . Por tanto, la desigualdad es cierta.
. Por tanto, la desigualdad es cierta.
20.-
Sean ![]() tres números
complejos tales que
tres números
complejos tales que ![]() . Demuestra que
. Demuestra que
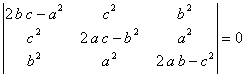
(Propuesto
por José Luís Díaz Barrero)
Solución
Si sustituimos ![]() por
por ![]() en el determinante, obtenemos:
en el determinante, obtenemos:

Ya que la suma de las tres filas es ![]()
Observación
Las filas del determinante cumplen la condición de los números, a+b+c=0