3. 2.- Problemas de la OIMU

11.- Sean m y n números enteros mayores que 1. Se definen los conjuntos y .

Encontrar la distancia entre y , que se define como

.

(18/11/2006-Problema 1)

Solución

En primer lugar es fácil ver que si entonces tomando

, y puesto que

.

Consideremos ahora el caso en que . Entonces demostraremos en primer lugar que . Para ello supongamos que existieran

Lo que nos lleva a una contradicción.

Por tanto

(Por ser el numerador entero positivo)

Demostremos que es exactamente igual a . Sabemos que la ecuación de Diofanto tiene infinitas soluciones con I, J enteros por ser precisamente . Entonces sólo nos hace falta ver que alguna de ellas cumple las restricciones . Para ello tomemos una solución cualquiera I, J. Por ser m y n estrictamente mayores que 1 sabemos que podemos escribirla como con . La prueba de que i, j han de ser distintos de cero es sencilla teniendo en cuenta que la ecuación está igualada a 1 y 1 no es divisible ni por n ni por m. Por tanto, tenemos que

. Es fácil demostrar que k ha de ser igual a l ya que si no sería estrictamente mayor que n, que es mayor que 1. (El que sea estrictamente mayor que n es porque, al ser , entonces :

Si , entonces , por lo que

Por tanto, si , entonces , por lo que

).

Por tanto tenemos que , siendo

, como queríamos, luego .

(Otra forma de ver que existen , tales que : La ecuación de congruencias tiene solución al ser , por lo que existe un tal que , con un número natural tal que .)

12.- Demostrar que para cualquier entero positivo n y cualesquiera números reales se cumple que la ecuación

, tiene al menos una raíz real.

(18/11/2006-Problema 2)

Solución

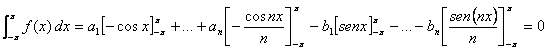(Al ser cos una función par, ). Entonces, al ser continua, existe un tal que (si entonces , si entonces . Por tanto, habrá algún tal que y algún tal que , luego por Bolzano habrá un entre medias tal que ).

Otra forma de verlo (análoga a la anterior): Una primitiva de sería

.

Se cumple que (ya que cos es una función par, ), por lo que, por el teorema de Rolle, existe un (en esta solución no hemos usado que es continua, sólo que tiene una primitiva que es continua en un intervalo cerrado, y que vale igual en sus extremos).

Observación

Se puede ver que la ecuación tiene al menos 2 soluciones reales en , ya que al ser una función del mismo tipo que , por lo que si y tiene una sola raíz en , entonces por continuidad de se cumplirá que , con sólo un tal que , por lo que , ó bien que , con sólo un tal que , por lo que , contradicción en ambos casos.

(De hecho la ecuación tiene infinitas soluciones reales, ya que , al ser y , por lo que es solución de la ecuación si lo es)

13.- Sean , para todo . Denotamos por el conjunto de todas las raíces reales de la ecuación . Demostrar que y que cada producto de dos elementos de es el promedio de dos elementos de .

(18/11/2006-Problema 2)

Solución

Para demostrar la segunda afirmación, vemos primero que la ecuación tiene todas las soluciones reales y en . Para ello, vamos a ver que la ecuación tiene todas las soluciones reales y en para todo tal que :

Observamos que el polinomio tiene grado , por lo que las ecuaciones , tienen soluciones:

Para , , polinomio de grado 3. Si suponemos que es un polinomio de grado , entonces , polinomio al ser composición de polinomios, y de grado .

Tenemos que ver entonces que las soluciones de son reales y en .

Para , cumple que . Tenemos que

, , , .

Entonces, va de a 1 cuando va de a , de 1 a cuando va de a , y de a 1 cuando va de a 1, por lo que cualquier recta con corta a en 3 puntos con la en .

Supongamos que tiene soluciones en para cualquier con . Entonces tiene como soluciones, como vimos para el caso , , , con para . Pero tiene soluciones en para (inducción), luego en total tiene soluciones en .

Entonces, para nos da que tiene raíces en , por lo que, por Rolle, tiene raíces en , una entre cada 2 raíces de , tantas entonces como el grado de . Si en una de ellas tiene un máximo relativo en la siguiente tiene un mínimo relativo y viceversa, ya que si en el intervalo tiene un máximo relativo, siendo raíces de , entonces para todo , por lo que si en el intervalo tiene otro máximo relativo, siendo otra raíz de , entonces para todo , por lo que en habría un mínimo relativo, contradicción con que las raíces de están entre las raíces de . Por tanto, en de las raíces de hay un máximo relativo de , y en las otras hay un mínimo relativo de , y en los máximos relativos es positiva, y en los mínimos relativos es negativa.

Vamos a ver que en los máximos relativos vale 1 y en los mínimos relativos vale :

Para ya lo vimos, en la demostración de que las soluciones de son reales y en .

Lo suponemos cierto para , entonces

, luego los extremos relativos de se alcanzan en los puntos donde se alcanzan los extremos relativos de , ó si vale ó

En los donde se alcanzan máximos relativos de , (inducción), por lo que , alcanzándose entonces también un máximo relativo de

En los donde se alcanzan mínimos relativos de , (inducción), por lo que , alcanzándose entonces también un mínimo relativo de

En los en los que , se cumple que , en los en los que , se cumple que .

Vemos ya que las soluciones de están todas en : Como para todo (es un punto fijo de ), el primer extremo relativo de , que se alcanzará en un punto , es un máximo (llamamos en general al punto donde se alcanza el extremo relativo número de ).

Entonces, como , , por Bolzano existe un tal que , como , , por Bolzano existe un tal que , y en general entre cada dos puntos donde se alcanza un extremo relativo de habrá una raíz de , luego habrá raíces de , que con , 1 (1 también es punto fijo de ) hacen raíces de , luego las soluciones de estarán todas en como queríamos ver, y serán por tanto del tipo coseno.

Vemos ahora que para todo :

Para ,

Si es cierto para ,

Vemos entonces cómo son las soluciones de :

, ó , con

. La primera ecuación da como solución , y la segunda da como solución , por lo que las soluciones de son , , con (aunque , el número de soluciones es finita por la periodicidad del coseno. Vimos que el número de soluciones era ).

Comprobamos que, si es solución de , entonces y son soluciones de . Que el coseno sea solución de ya lo vimos al demostrar la primera afirmación, cuando vimos que .

Para demostrar que el seno también es solución, vemos primero que es solución de si par:

, solución de como vimos antes, al pertenecer 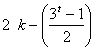a , ya que como es par , por lo que es múltiplo de 4.

Entonces, si tenemos una solución de del tipo , se cumple que 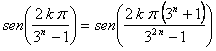, solución de como hemos visto antes, al ser par.

Si tenemos una solución de del tipo , se cumple que 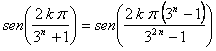, solución de como hemos visto antes, al ser par.

Utilizamos todo esto para ver que, si , son soluciones a , entonces , son soluciones a :

Donde la penúltima igualdad se debe a que, como , son soluciones a , por lo visto antes , , , son soluciones a , y entonces ,…

De igual forma,

Entonces, si , son soluciones de , se cumple que:

, promedio de dos soluciones de

.

Otra forma de hallar las soluciones de en la que no hace falta ver que están todas en :

Si probamos soluciones a esta ecuación del tipo coseno, vimos que éstas han de ser y , con . Pero por la periodicidad del coseno, vemos que todas las soluciones son , , con , .

Pero basta con llegar a y , ya que si , tenemos que , por lo que

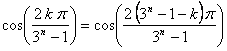, con , y lo mismo pasaría para . Como , están entre 0 y cuando está entre 0 y , está entre 0 y , y ahí el coseno es inyectivo, las soluciones con entre 0 y son distintas entre sí y las soluciones con entre 0 y son distintas entre sí, por lo que en principio tenemos soluciones a la ecuación. Pero no todas las de la forma son distintas a las de la forma , ya que si , los cosenos son iguales. Esto pasa cuando .

Como (si y , entonces ), la única opción para que se dé esta igualdad con entre 0 y y entre 0 y es ó y , por lo que hay que descontar 2 soluciones y en realidad hay soluciones distintas a la ecuación. Como vimos que el grado de es , éstas son todas las soluciones a (son por tanto con , con )

Otra forma de ver que, si , son soluciones a , entonces , son soluciones a :

Si son soluciones a de la forma y , con , entonces , con , luego también es solución a , y por tanto a como vimos, y lo mismo pasará con

.

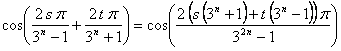Tendremos el mismo caso si las soluciones iniciales son de la forma y . Si las soluciones iniciales son de la forma y , con , entonces , con

, luego será solución de , y lo mismo pasará con

14.- Sea un número entero mayor que 1, no divisible ni por 2 ni por 5. En la escritura decimal infinita del número se eligen arbitrariamente un número finito de dígitos después del punto decimal y luego se borran. Claramente el número decimal obtenido es racional también y por lo tanto tiene la forma con y enteros. Demostrar que es divisible por .

(2008-Problema 1)

Solución

Si es periódico puro de la forma resulta:

Restando ambas expresiones llegamos a

.

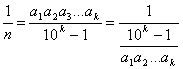Si al borrar un número finito de dígitos es periódico puro entonces y hemos terminado. Si es periódico mixto entonces se puede escribir de la forma y tenemos:

Restando ambas expresiones tenemos:

, es decir,

De donde resulta:

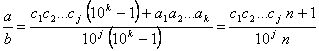
(en la última igualdad hemos dividido numerador y denominador entre y hemos tenido en cuenta que ). Entonces, como es primo relativo con el numerador, divide a .

Si es periódico mixto de la forma , operando de la misma manera resulta

.

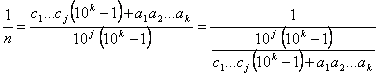Pero como no es divisible entre 10 tenemos que para algún natural. Sustituyendo este valor en la expresión anterior resulta 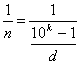y como tenemos que , por lo que podemos poner y la expresión queda . Consideremos ahora el número periódico puro , resulta (razonando como al principio):

Por lo que restando ambas expresiones se sigue que . De aquí se deduce que y por tanto es periódico puro, contradicción, por lo que no puede ser periódico mixto.

Queda demostrar que la expresión no puede tener un número finito de cifras decimales con las condiciones del enunciado. Si suponemos que esto es posible resulta , luego . Como la parte derecha de la expresión es entera, la parte izquierda también debe serlo por lo que divide a , pero esto es imposible ya que por el enunciado se tiene que no es divisible ni entre 5 ni entre 2.

15.- Demostrar que para cada número natural existe un polinomio con coeficientes reales, de grado , tal que el polinomio es divisible por en el anillo .

(2008-Problema 2)

Solución

Sea , si tomamos resulta que:

.

Es evidente que dichos polinomios verifican el enunciado para todo .

16.- Dos vértices A y B de un triángulo ABC están ubicados en una parábola con de tal forma que los lados AC y BC son tangentes a la parábola. Sea la longitud de la mediana del triángulo ABC y S el área de dicho triángulo. Encontrar .

(2008-Problema 4)

Solución

Tenemos que las coordenadas de los vértices A y B son , . C viene dado por la intersección de las rectas:

,

de donde resulta:

.

Esta ecuación tiene como solución . Sustituyendo obtenemos que:

Por otro lado, las coordenadas del punto medio del segmento AB son:

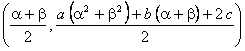, de donde se deduce que la mediana es paralela al eje OY y su longitud es:

Por otra parte tenemos que y

, por lo que la superficie del triángulo ABC viene dada por

(Suponemos sin pérdida de generalidad que ). Finalmente el resultado pedido es:

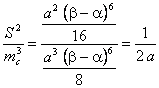
17.- Sean  y  dada por , donde . Encontrar el valor máximo de

(2009-Problema 3)

Solución

Si extendemos la definición de a  (cierre de ), por el teorema de Weierstrass  tendrá máximo en  al ser una función continua (polinomio) definida en un compacto.

En  se cumple que:

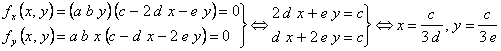, por lo que 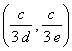 es el único punto crítico de , con:

En la parte de la frontera de  contenida en los ejes se cumple que , al tener  el factor , en la parte de la frontera de  contenida en  se cumple que , al tener  el factor , por lo que el máximo absoluto de  en  se alcanza en .

Como  (ya que , , ), el máximo absoluto de  en  se alcanza en , siendo su valor

18.- Sean  tales que . Demostrar que:

(2007-Problema 3)

Solución

Sustituyendo  por  en la desigualdad, ésta queda:

. Desarrollando lo de la izquierda, llegamos a

 (al ser ).

Desarrollando nuevamente lo de la izquierda, llegamos a:

.

Pero se cumple que:

(al ser ). Esta última ecuación tiene como soluciones:

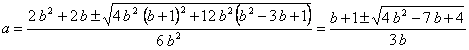
(la última igualdad es porque . Las soluciones son reales al ser el discriminante de  igual a , por lo que ).

Tenemos que  si  ó ,

 si , por lo que el único punto crítico que es máximo relativo es .

 Entonces, el máximo absoluto de  en  puede estar en  ó en  (existe el máximo absoluto de  en  al ser  continua por ser polinomio y cumplirse que ).

Pero  (al ser  , con  si ,  si , por lo que el máximo absoluto de  en  se alcanza en 1, y ),

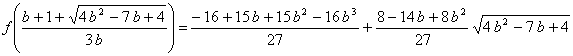
Vemos que esta cantidad es también menor ó igual que 0. Esto es equivalente a ver que

(al ser  como vimos antes, )

Si desarrollamos los productos, pasamos todos los términos a la derecha, simplificamos y quitamos factores positivos comunes, nos queda que la desigualdad anterior es equivalente a . Se puede ver por Ruffini que  tiene la raíz 1 doble, factorizándose como . Pero el discriminante de  es , siendo el coeficiente de  positivo, por lo que  y entonces  para todo  como queríamos. Entonces el máximo absoluto de  es menor ó igual que 0, por lo que  para todo  y entonces  para todo  como queríamos.

(La igualdad se alcanzará cuando el máximo absoluto de  se alcance en  y sea 0, que será cuando:

, es decir, cuando  y entonces =1, ).

19.- Demostrar la desigualdad  para

(2008-Problema 3)

Solución

Si llamamos , tenemos que

(ya que 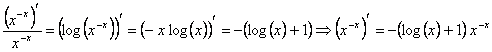), , por lo que el signo de  es el mismo que el de .

Se cumple que, con:

(hemos aplicado L’Hopital en la tercera igualdad y en la quinta), , ,

. Como  en los puntos críticos y en los extremos es menor ó igual que 0, se cumple que el máximo absoluto de la prolongación de  a  es 0 y se alcanza en , por lo que  si  y entonces  si , lo que implica que  es estrictamente decreciente en  con . Por tanto  si y  es estrictamente creciente en  con , lo que lleva a que  si , como queríamos.

20.- Hallar todos los números enteros positivos  para los cuales existen números enteros positivos , …, , , …,  tales que

(2008-Problema 3)

Solución

La ecuación se puede escribir como

Como  es un número natural si , puede haber como mucho términos  no nulos.

Ahora, si en  definimos la relación  si , tenemos que  es una relación de equivalencia:

 porque , luego  es reflexiva.

Si  tenemos que , por lo que , luego  y  es simétrica.

Si  y  tenemos que ,   por lo que , , luego , por lo que  y  es transitiva.

Entonces, si hay  clases de equivalencia con , …,  elementos, será , y el número de términos  no nulos será:

 (número de formas de tomar  de clases de equivalencia distintas).

Tenemos por tanto que, si  para algún , como , , …, , será , siendo la desigualdad estricta por la condición  para algún . Por tanto, el número de términos  no nulos será mayor que , contradicción con lo anterior.

Entonces  para todo , por lo que  y

Si , la ecuación inicial queda , imposible.

Si , la ecuación inicial se puede escribir como  , imposible ya que 2 no es un cuadrado perfecto.

Si , la ecuación inicial se puede escribir como:

, teniendo como solución única:

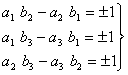. Éste es un sistema en  con determinante de la matriz de coeficientes 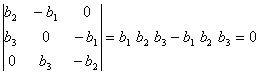, por lo que para que tenga

solución ha de ser:

, ,  (es decir, uno de los  ha de ser suma de los otros dos). Por tanto, uno de los  ha de ser suma de los otros dos (sustituyendo la relación de  en , y teniendo en cuenta la expresión de ). Una solución que cumple esto es , , , , :

Efectivamente, (cualquier permutación igual de los  y de los  da otra solución). Por tanto, es el único valor posible.

Observaciones

1) Como no hemos utilizado el hecho de que los ,  sean positivos para descartar los valores  (sólo hemos usado que los ,  son enteros no nulos), hemos demostrado un resultado más general que el que se desprende del enunciado:

el único valor de  para el que la ecuación:

tiene soluciones enteras no nulas es . En este caso, la ecuación admite soluciones con los ,  naturales, como la mostrada anteriormente.

2) Para  la ecuación tiene infinitas soluciones con ,  naturales:

, , ,  es solución, con ,  naturales si ,  son naturales.

Indice Siguiente