2.
4.- Interpretaciones Geométricas
Una de las estrategias más
importantes para afrontar un problema matemático es la capacidad de
visualizarlo, de interpretarlo físicamente, geométricamente o desde otra
perspectiva distinta de aquella con la que está propuesto. Muchas veces, la
interpretación del problema desde otro campo hace que convirtamos un problema
difícil en uno que ya sabemos resolver, o que podemos resolver con más
facilidad.
Usaremos como ejemplo la
siguiente desigualdad:
Tomemos un vector con componentes
positivas 
. Probar que el módulo del vector es menor que 
.
Supongamos que k es el módulo del vector. Entonces
tenemos que 
y por
tanto los números k, x, y
son, por el teorema de Pitágoras, los lados de un triángulo rectángulo. Por
tanto es evidente por la desigualdad triangular que cada uno de los lados tiene
que ser menor que la suma de los otros dos y en particular 
.
Vemos otro ejemplo de interpretación geométrica:
Sean 
, 
, 
, tres números
naturales arbitrarios
a) Demostrar que la expresión
, es un entero.
b) Supongamos que 
. En estas condiciones, ¿es necesario que 
para que 
? ¿Es suficiente dicha condición para que ?
(Propuesto en el Concurso Puig-Adam)
a) Si desarrollamos la expresión vemos que:
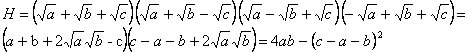
Que evidentemente es un entero.
b) Vemos que es
suficiente: Si , 
, por lo que 
. También sabemos que 
. Siempre que tenemos un número positivo mayor que otros 2,
pero menor que la suma de esos 2, podemos construir un triángulo de lados esos
3 números: Basta con tomar un segmento de longitud el mayor de los 3, y hacer
las circunferencias de centros los extremos del segmento y radios los otros 2
números. Las circunferencias se intersecan en un punto que, con los 2 extremos
del segmento, hacen un triángulo de lados los 3 números (ver figura). Entonces
existe un triángulo de lados 
. Por la fórmula de Heron, el área de este triángulo será
.
Para que exista, lo de dentro de la raíz (
) ha de ser 
.
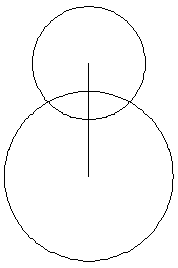
Figura: El triángulo con vértices los 2 del segmento y una de las intersecciones entre las 2 circunferencias tiene lados 2, 3, 4, si la longitud del segmento es 4 y los radios de las circunferencias 2 y 3.
Tomando 
,
y 
, se cumple que:
, pero 
, luego la condición no es necesaria.
Observación
Como se puede ver, lo que se ha hecho ha sido interpretar el
enunciado como que eran los lados de un
triángulo, y entonces con una fórmula conocida (la fórmula de Heron) el
problema era inmediato.
Otro problema de mayor dificultad que los anteriores es el siguiente:
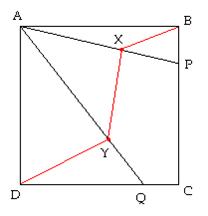
Tenemos un cuadrado de vértices A, B,
C, D. Se trazan las líneas AP y AQ sabiendo que BP=CQ. Se escogen dos puntos
cualesquiera X, Y en dichas rectas. Demostrar que siempre se puede construir un
triángulo de lados BX, XY, YD
(Propuesto en la OIM-2003)
Para solucionarlo,
usaremos la siguiente idea:
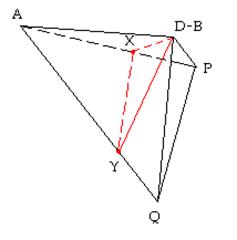
Si
doblamos el cuadrado tal y como muestra el dibujo, el triángulo queda formado
en el espacio ya que AD=AB y por tanto
coinciden. Sólo queda demostrar que el tetraedro dibujado siempre se podrá formar,
para lo cual basta con demostrar que el ángulo PAQ es menor o igual que 45º,
que es cierto por ser BP=CQ, ya que el
ángulo QAC<PAB.
Observación
Existe una solución analítica del problema, muy tediosa. Sin
embargo una idea tan sencilla como la que hemos explicado arriba permitía dar
una solución muy elegante.
Aunque estas estrategias normalmente no suelen tener
aplicación directa en los problemas, sí queremos insistir en que pueden
facilitar un problema más difícil, ó darnos ideas para enfocarlo.
Por último, pensemos el siguiente problema:
Sean 
números reales y sea 
. Demostrar que 
.
Si consideramos la siguiente figura:
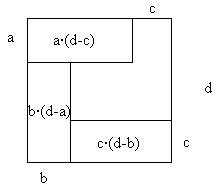
Entonces el área del cuadrado es justamente 
y los tres rectángulos
tienen área 
que siempre será menor
que el área del cuadrado con igualdad si y solamente si 
, ó cualquier otra permutación.
Este problema se propuso en una preparación para la olimpiada
internacional a varios alumnos de 4º de E. S. O. Sorprendentemente, todos ellos
lo solucionaron de esta forma. Cuando se les preguntó en qué razonamientos se
habían basado para llegar a esa solución, dijeron que el segundo miembro de la
desigualdad, el les había hecho
pensar en el área de un cuadrado,
mientras que los otros términos eran productos de dos números distintos y
positivos y por tanto podían ser interpretados como áreas de rectángulos.
Bastaba entonces con pintar el cuadrado de lado d y tratar de encajar en él los rectángulos.